C Program Fft Algorithm

As discussed in Chapter 8, the real DFT can be calculated by correlating thetime domain signal with sine and cosine waves (see Table 8-2). Table 12-2shows a program to calculate the complex DFT by the same method. In anapples-to-apples comparison, this is the program that the FFT improves upon.Tables 12-3 and 12-4 show two different FFT programs, one in FORTRAN andone in BASIC.

First we will look at the BASIC routine in Table 12-4. Thissubroutine produces exactly the same output as the correlation technique inTable 12-2, except it does it much faster.

Fft Algorithm Tutorial

The block diagram in Fig. 12-7 canbe used to identify the different sections of this program. Data are passed to thisFFT subroutine in the arrays: REX and IMX , each running from sample 0to N-1. Upon return from the subroutine, REX and IMX are overwrittenwith the frequency domain data. This is another way that the FFT is highlyoptimized; the same arrays are used for the input, intermediate storage, andoutput.

This efficient use of memory is important for designing fast hardwareto calculate the FFT. The term in-place computation is used to describe thismemory usage.While all FFT programs produce the same numerical result, there are subtlevariations in programming that you need to look out for.

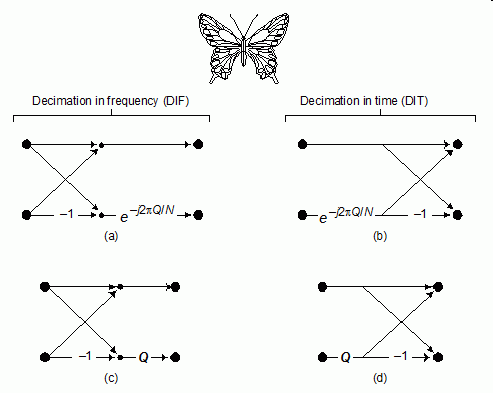
Several of these. Important differences are illustrated by the FORTRAN program listed in Table12-3. This program uses an algorithm called decimation in frequency, whilethe previously described algorithm is called decimation in time. In adecimation in frequency algorithm, the bit reversal sorting is done after thethree nested loops. There are also FFT routines that completely eliminate thebit reversal sorting. None of these variations significantly improve theperformance of the FFT, and you shouldn't worry about which one you areusing.The important differences between FFT algorithms concern how data are passedto and from the subroutines.

In the BASIC program, data enter and leave thesubroutine in the arrays REX and IMX , with the samples running fromindex 0 to N-1. In the FORTRAN program, data are passed in the complexarray X( ), with the samples running from 1 to N. Since this is an array ofcomplex variables, each sample in X( ) consists of two numbers, a real part andan imaginary part.

The length of the DFT must also be passed to thesesubroutines. In the BASIC program, the variable N% is used for this purpose.In comparison, the FORTRAN program uses the variable M, which is definedto equal Log 2 N. For instance, M will be. 8 for a 256 point DFT, 12 for a 4096 point DFT, etc. The point is, theprogrammer who writes an FFT subroutine has many options for interfacingwith the host program. Arrays that run from 1 to N, such as in the FORTRANprogram, are especially aggravating. Most of the DSP literature (including thisbook) explains algorithms assuming the arrays run from sample 0 to N-1.

Forinstance, if the arrays run from 1 to N, the symmetry in the frequency domainis around points 1 and N/2 + 1, rather than points 0 and N/2.Using the complex DFT to calculate the real DFT has another interestingadvantage. The complex DFT is more symmetrical between the time andfrequency domains than the real DFT. That is, the duality is stronger. Amongother things, this means that the Inverse DFT is nearly identical to the ForwardDFT.

In fact, the easiest way to calculate an Inverse FFT is to calculate aForward FFT, and then adjust the data. Table 12-5 shows a subroutine forcalculating the Inverse FFT in this manner.Suppose you copy one of these FFT algorithms into your computer program andstart it running. How do you know if it is operating properly? Two tricks arecommonly used for debugging. First, start with some arbitrary time domainsignal, such as from a random number generator, and run it through the FFT.Next, run the resultant frequency spectrum through the Inverse FFT andcompare the result with the original signal. They should be identical, exceptround-off noise (a few parts-per-million for single precision).The second test of proper operation is that the signals have the correct symmetry.When the imaginary part of the time domain signal is composed of all zeros (thenormal case), the frequency domain of the complex DFT will be symmetricalaround samples 0 and N/2, as previously described.